Division (भाग संक्रिया)
Introduction:
The traditional method of division is of the following form.
Quotient
_______
Divisor) Dividend ó Divisor) Dividend (Quotient
----------
---------- ----------
_________ _________
Remainder Remainder
But in the Vedic process, the format is
Divisor) Dividend
--------
--------
__________________
Quotient / Remainder
- Traditional Method (परम्पारगत विधि)
Example: Divide 1697 by 14
14) 1697 (121
14
_____
29
28
_____
17
14
_____
03
Thus Q = 121 and R = 03
- Nikhilam (निखिलम्)
- Think about any two digit numbers (dividends) and divisor 9. Notice the following example.
- 14 ÷ 9
9) 14 (1
9
____
5
The quotient (Q) is 1; Remainder (R) is 5.
- 35÷9, Q is 3, R is 8.
- 50÷9, Q is 5, R is 5.
Now we have different type of representation for the above examples as given:
- Split dividend into a left-hand part for the Quotient and right-hand part for the remainder by a slash.
14 as 1/4, 35 as 3/5, 50 as 5/0
- Leave some space below such representation, draw a horizontal line.
1/4, 3/5 5/0
______, ______, ______
iii. Put the first digit of the dividend as it is under the horizontal line. Put the same digit under the right hand part for the remainder; add the two and place the sum, sums of the digits of the numbers as the remainder.
1/4 3/5 5/0
1 3 5
______, ______, ______
1/5 3/8 5/5
Now the problem is over.
14 ÷ 9 gives Q = 1, R = 5
35 ÷ 9 gives Q = 3, R = 8
50 ÷ 9 gives Q = 5, R = 5
The examples given so far convey that in the division of two digit numbers by 9, we take the first digit down for the quotient–column and that, by adding the quotient to the second digit, we can get the remainder.
- Now in the case of 3 digit numbers, let us proceed as follows.
9) 105 (11 9) 10/5
99 1/1
¯¯¯¯¯¯ ó ¯¯¯¯¯¯¯
6 11/6
9) 211 (23 9) 21/1
207 2/3
¯¯¯¯¯ ó ¯¯¯¯¯¯¯
23/4
Note that the first digit of the dividend from left is added mechanically to the second digit of the dividend to obtain the second digit of the quotient. This digit added to the third digit sets the remainder. The first digit of the dividend remains as the first digit of the quotient.
Example: 134 ÷ 9
The first digit of the dividend 1 is first digit of the quotient. Add the first digit 1 to second digit 3 getting second digit of quotient, which is 1 + 3 = 4. Hence Quotient is 14. Now second digit of 14 i.e., 4 is added to third digit 4 of dividend to get the remainder 8 (4 + 4)
9) 13/4
1/4
______
14/8
Q is 14, R is 8.
- extending the same principle even to bigger numbers of still more digits, we can get the results.
Example:
1204 ÷ 9
- Add first digit 1 to the second digit 2, 1 + 2 = 3
- Add the second digit of quotient 13, 3 to third digit ‘0’ and obtain the Quotient. 3 + 0 = 3, 133
iii. Add the third digit of Quotient 133, 3 to last digit ‘4’ of the dividend and write the final Quotient and Remainder.
R = 3 + 4 = 7, Q = 133
In symbolic form
9)120/4
13/3
_____
133/7
When remainder is greater than divisor, it can also be represented as
Example:
247÷ 9
9)24/7
2/6
_______
26/1/3
/1
_______
1/4
_______
27/4
Quotient=27; Remainder=4.
- Now consider the divisors of two or more digits. Nikhilam rule comes to rescue us. The nikhilam states “all from 9 and the last from 10”.
यदि भाजक में 5 से बड़े अंक हो तो भाग संक्रिया में सूत्र ‘निखिलम्’ आधारित विधि उपयोगी होती हैं।
सूत्र आधारित विधि -
- भाजक के निकटतम आधार को निर्धारित कर पूरक संख्या ज्ञात करते हैं।
- भाग क्रिया के निर्धारित स्थान को दो खड़ी रेखाओं द्वारा तीन खण्ड़ों में बांटते हैं।
- बायीं ओर से पहले खण्ड़ में भाजक तथा उसके नीचे पूरक संख्या लिखते हैं।
- आधार में जितने शून्य हो उतने ही अन्तिम अंक तीसरे खण्ड़ में लिखते हैं, तथा शेष अंक मध्य खण्ड़ में लिखते हैं।
- क्रिया विधि -
- मध्य खण्ड़ का पहला अंक नीचे योग के स्थान पर लिखते हैं।
- इस अंक को पूरक संख्या से गुणा कर मध्य खण्ड़ के दूसरे अंक के नीचे लिखते हैं, यदि गुणनफल में दो अंक हो तो दूसरे अंक को तीसरे अंक के नीचे लिखते हैं। केवल दूसरे स्थान के ऊपर नीचे के अंकों को जोड़कर योग को योगफल के स्थान पर लिख देते हैं, तीसरे स्थान के अंकों को इस पद में नही जोड़ते हैं।
- प्राप्त योग अंक को पुनः पूरक संख्या से गुणा कर गुणनफल को भाज्य के तीसरे अंक के नीचे लिख कर जोड़ देते हैं।
- यह प्रक्रिया तब तक दोहराते हैं, जब तक कि गुणनफल के अंक तीसरे खण्ड़ के अन्तिम अंक के नीचे तक नही लिख दिये जायें।
- अंत में जोड़ने पर मध्य खण्ड़ के नीचे लिखा योग, भागफल तथा तीसरे खण्ड़ के नीचे लिखा योग, शेषफल कहलाता हैं।
- यदि शेषफल भाजक से बड़ा हो तो उसमें से भाजक घटा कर भागफल तथा शेषफल का संशोधित मान ज्ञात करते हैं।
Example: 1245÷97
|
|
संकेत- 1. भाजक = 97, आधार = 100, पूरक संख्या = 03, प्रथम खण्ड़ में भाजक तथा पूरक संख्या लिखते हैं। 2. तृतीय खण्ड़ में 45 तथा मध्य खण्ड़ में 12 लिखते हैं। 3. मध्य खण्ड़ का 1 नीचे योग के स्थान पर लिखते हैं। 4. यह अंक (1) X पूरक संख्या (0) = 0, मध्य खण्ड़ के 2 के नीचे लिखते हैं। तथा (1) X पूरक संख्या (3) = 3, तृतीय खण्ड़ के 4 के नीचे लिखते हैं। |
|
5. योग = 2 + 0 = 2, नीचे योग के स्थान पर लिखते हैं। 6. यह अंक (2) X पूरक संख्या (0) = 0, तृतीय खण्ड़ के 4 के नीचे लिखते हैं। तथा (2) X पूरक संख्या (3) = 6, तृतीय खण्ड़ के 5 के नीचे लिखते हैं। 7. योग = 4 + 3 + 0 = 7, तथा = 5 + 6= 11 8. संशोधित शेषफल = 7 + 1 = 8 तथा 1, नीचे योग के स्थान पर लिखते हैं। 9. भागफल = 12, शेषफल = 81 |
|
- Paravartya-yojayet (परावर्त्य योजयेत्)
‘Paravartya–Yojayet’ means 'transpose and apply'
चिन्ह परिवर्तित कीजिये तथा प्रक्रिया प्रारम्भ कीजिये।
- Consider the division by divisors of more than one digit, and when the divisors are slightly greater than powers of 10.
यदि भाजक में 5 से छोटे अंक हो तो भाग संक्रिया में सूत्र ‘परावर्त्य योजयेत्’ आधारित विधि उपयोगी होती हैं।
सूत्र आधारित विधि -
- भाजक के निकटतम आधार को घटाकर विचलन ज्ञात करते हैं। यह विचलन पूरक संख्या का ॠणात्मक मान होता हैं।
- विचलन के प्रत्येक अंक का चिन्ह परिवर्तित कर परावर्तित अंक प्राप्त करते हैं।
- भाग क्रिया के निर्धारित स्थान को दो खड़ी रेखाओं द्वारा तीन खण्ड़ों में बांटते हैं।
- बायीं ओर से पहले खण्ड़ में भाजक, उसके नीचे विचलन तथा विचलन के नीचे परावर्तित अंक लिखते हैं।
- आधार में जितने शून्य होते हैं, भाज्य के उतने ही अन्तिम अंक तीसरे खण्ड़ में लिखते हैं।
- क्रिया विधि -
- मध्य खण्ड़ का पहला अंक नीचे योग के स्थान पर लिखते हैं।
- इस अंक को परावर्तित अंक से गुणा कर मध्य खण्ड़ के दूसरे अंक के नीचे लिखते हैं, यदि गुणनफल में दो अंक हो तो दूसरे अंक को तीसरे अंक के नीचे लिखते हैं। केवल दूसरे स्थान के ऊपर नीचे के अंकों को जोड़कर योग को योगफल के स्थान पर लिख देते हैं, तीसरे स्थान के अंकों को इस पद में नही जोड़ते हैं।
- प्राप्त योग अंक को पुनः परावर्तित अंक से गुणा कर गुणनफल को भाज्य के तीसरे अंक के नीचे लिख कर जोड़ देते हैं।
- यह प्रक्रिया तब तक दोहराते हैं, जब तक कि गुणनफल के अंक तीसरे खण्ड़ के अन्तिम अंक के नीचे तक नही लिख दिये जायें।
- अंत में जोड़ने पर मध्य खण्ड़ के नीचे लिखा योग, भागफल तथा तीसरे खण्ड़ के नीचे लिखा योग, शेषफल कहलाता हैं।
- यदि शेषफल भाजक से बड़ा हो तो उसमें से भाजक घटा कर भागफल तथा शेषफल का संशोधित मान ज्ञात करते हैं।
Example: Divide 1697 by 14
|
|
संकेत- 1. Write the Divisor leaving the first digit, writes the other digit or digits using negative (-) sign and place them below the divisor as shown. 2. Write down the dividend to the right. Set apart the last digit for the remainder. 3. Write the 1st digit below the horizontal line drawn under the dividend. Multiply the digit by –4, write the product below the 2nd digit and add. Since 1 x –4 = -4 and 6 + (-4) = 2 4. We get second digits’ sum as ‘2’. Multiply the second digits’ Sum thus obtained by –4 and writes the product under 3rd digit and Add. |
|
5. Continue the process to the last digit. 6. The sum of the last digit is the Remainder and the result to its left is Quotient. 7. Thus Q = 121 and R = 3 |
|
Example: (a) Divide 32894 by 1028
|
|
संकेत- 1. भाजक = 1028, आधार = 1000, विचलन = 028 (तीन अंक) 2. परावर्तित अंक = 0-2-8 (तीन अंक) 3. तृतीय खण्ड़ में 894 तथा मध्य खण्ड़ में 32 लिखते हैं। 4. मध्य खण्ड़ का 3 नीचे योग के स्थान पर लिखते हैं। |
|
5. यह अंक (3) X परावर्तित अंक (0) = 0, मध्य खण्ड़ के 2 के नीचे 0 लिखते हैं। (3) X (-2) = -6, तृतीय खण्ड़ के 8 के नीचे -6 लिखते हैं। व (3) X (-8) = -24, तृतीय खण्ड़ के 9 के नीचे -24 लिखते हैं। 6. योग = 2 + 0 = 2, मध्य खण्ड़ में नीचे योग के स्थान पर लिखते हैं। 7. यह योग अंक (2) X परावर्तित अंक (0) = 0, तृतीय खण्ड़ के 8 के नीचे 0 लिखते हैं। (2) X (-2) = -4, तृतीय खण्ड़ के 9 के नीचे -4 लिखते हैं। तथा (2) X(-8) = -16, तृतीय खण्ड़ के 4 के नीचे -16 लिखते हैं। 8. योग = [8+(-6)+0=2], [9+(-24)+(-4)=19] व [4+(-16) = -12], नीचे योग के स्थान पर लिखते हैं। 9. शेषफल में ॠणात्मक संख्याऐं -19 तथा -12 हैं, इस स्थिति का समाधान करने के लिए भागफल वाले भाग से 1 घटा लेते हैं, जिससे भागफल = 32-1 = 31 हो जाता हैं तथा शेषफल के स्थानीय मान को भाजक में से घटाकर संशोधित शेषफल प्राप्त करते हैं। शेषफल = 1028+(2x100)+(-19x10)+(-12x1) = 1028+200-190-12 = 1228-202 = 1026 भागफल = 31, शेषफल = 1026 |
|
इसी उदाहरण को अन्य विधि द्वारा भी हल किया जा सकता हैं।
(b)
 |
संकेत- भागफल = 32-1=31 शेषफल = 1028+(2x100)+(-19x10)+(-12x1) =1028+200-190-12 =1228-202 =1026 भागफल = 31, शेषफल= 1026 |
(c) भाजक को ॠणात्मक संख्या (vinculum no.) में बदलने पर 1028 =  प्राप्त होता हैं।
प्राप्त होता हैं।
 |
संकेत- भागफल = 31, शेषफल= 1026 |
(d) भाज्य को ॠणात्मक संख्या (vinculum no.) में बदलने पर 32894 =  प्राप्त होता हैं।
प्राप्त होता हैं।
 |
संकेत- भागफल = 31, शेषफल= 1026 |
Example: Divide 1234 by 112
|
|
संकेत- 1. भाजक =112, आधार =100, विचलन =12 (दो अंक) 2. परावर्तित अंक = -1-2 (दो अंक) 3. अतः तृतीय खण्ड़ में 34 तथा मध्य खण्ड़ में 12 लिखते हैं। 4. मध्य खण्ड़ का 1 नीचे योग के स्थान पर लिखते हैं। 5. यह अंक (1) X परावर्तित अंक (-1) = -1, मध्य खण्ड़ के 2 के नीचे -1 लिखते हैं। तथा (1) X (-2) = -2, तृतीय खण्ड़ के 3 के नीचे -2 लिखते हैं। |
|
6. योग = 2 + -1 = 1, मध्य खण्ड़ में नीचे योग के स्थान पर लिखते हैं। 7. यह योग अंक (1) X परावर्तित अंक (-1) = -1, तृतीय खण्ड़ के 3 के नीचे -1 लिखते हैं। तथा (1) X (-2) = -2, तृतीय खण्ड़ के 4 के नीचे -2लिखते हैं। 8. योग = [3 +(-2)+(-1) = 0], व [4 +(-2) = 2], नीचे योग के स्थान पर लिखते हैं। 9. भागफल = 11, शेषफल= 02 |
|
Example: Divide 14885 by 123
 |
संकेत- 1. भाजक =123, आधार =100, विचलन =23 (दो अंक) 2. परावर्तित अंक = -2-3 (दो अंक) 3. हल करने पर - भागफल = 121, शेषफल = 02 |
Example: Divide 13456 by 1123
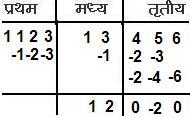 |
संकेत- शेषफल वाले भाग में ॠणात्मक मान -20 हैं, इस स्थिति का समाधान करने के लिए भागफल वाले भागमें से 1 घटा लेते हैं, तथा शेषफल -20 को भाजक में से घटाकर संशोधित शेषफल प्राप्त करते हैं। भागफल = 12-1 = 11, शेषफल = 1123-20 = 1103 |
- urdhva-tiryak and Dhvjanka (ऊर्ध्व-तिर्यक एवं सूत्रध्वजांक)
Here is another process of division based on the combination of Vedic sutras urdhva-tiryak and Dhvjanka. Dhvjanka means “on the top of the flag"
इस विधि में ‘ऊर्ध्व-तिर्यग्भ्याम् एवं ध्वजांक’ का प्रयोग किया जाता हैं। ध्वजांक का अर्थ ‘ध्वज के समान ऊपर रखी संख्या’ होता हैं।
सूत्र आधारित विधि -
- सर्वप्रथम भाजक को दो भागों में विभाजित करते हैं,भाजक के इकाई युक्त अंक को ध्वजांक तथा शेष भाग को मुख्यांक या संशोधित भाजक कहते हैं। ध्वजांक में केवल इकाई युक्त कई अंक हो सकते हैं।
- भाग क्रिया के निर्धारित स्थान को दो खड़ी रेखा द्वारा तीन खण्ड़ों में बांटते हैं।
- बायीं ओर से पहले खण्ड़ में भाजक के दोनों भाग लिखते हैं। मुख्यांक या संशोधित भाजक को नीचे अर्थात् आधार स्थान पर तथा ध्वजांक को उससे ऊपर अर्थात घातांक के स्थान पर लिखते हैं।
- ध्वजांक में जितने अंक होते हैं, भाज्य के उतने ही अन्तिम अंक तीसरे खण्ड़ में तथा शेष अंक मध्य खण्ड़ में लिखते हैं।
- क्रिया-विधि-

a मध्य खण्ड़ में लिखे भाज्य के सबसे बायें अंक में मुख्यांक का भाग देने पर भागफल का जो प्रथम अंक आता हैं, उसे नीचे भागफल के निर्धारित स्थान पर लिखते हैं।
b शेषफल को मध्य खण्ड़ के दूसरे अंक से पहले और नीचे लिखते हैं, जो नया भाज्य बनाता हैं।
c नये भाज्य से निम्न सूत्र द्वारा संशोधित भाज्य प्राप्त करते हैं।
संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक)
d संशोधित भाज्य में मुख्यांक का फिर भाग देकर प्रक्रिया को पुनः दोहराते हैं। भाग क्रिया पूर्ण होने पर भागफल तथा शेषफल प्राप्त हो जाते हैं।
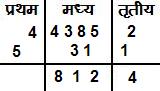
Example: 43852 ÷ 54
|
|
संकेत- 1. Put down the first digit (5) of the divisor (54) in the divisor column as operator and the other digit (4) as flag digit. Separate the dividend into two parts, one digit in right part. This is because the flag digit is single digit. 2. (a) Divide 43 by the operator 5. Now Q= 8 and R = 3. Write this Q=8 as the 1st Quotient-digit and R=3, the prefix for the next digit, 8 of the dividend. This 38 becomes the gross-dividend (G.D.) for the next step. (b) Subtract the product of flag digit (4) and first quotient digit (8) from the G.D. (38) i.e. 38-(4X8) =38-32=6. Now 6 is the net-dividend (N.D) for the next step. |
|
3. 6 ÷ 5, Q = 1, R = 1. So Q = 1, the second quotient-digit and R = 1, the prefix for the next digit 5 of the dividend. 4. Now G.D = 15; product of flag-digit (4) and second quotient digit (1) is 4X1=4 Hence N.D=15-4=11 divide N.D by 5 to get 11 ÷ 5, Q = 2, R= 1. 5. The final remainder is obtained by subtracting the product of flag-digit (4) and third quotient digit (2) form 12, Final remainder = 12 - (4 X 2) = 12 - 8 = 4. 6. Quotient = 812 and Remainder = 4. |
|
Example: 237963 ÷ 524
|
|
संकेत- 1. 524 में से 5 को मुख्यांक तथा 24 को ध्वजांक लेते हैं। भाज्य के अन्तिम दो अंक तीसरे खण्ड़ में तथा शेष अंक मध्य खण्ड़ में लिखते हैं। 2. मध्य खण्ड़ के 23 में 5 का भाग देते हैं। |
|
3. भागफल = 4 को रेखा के नीचे लिखते हैं, यह भागफल का प्रथम अंक होगा तथा शेषफल = 3 को मध्य खण्ड़ के 7 से पहले तथा नीचे लिखते हैं। अतः नया भाज्य = 37 होगा। 4. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 37-(4X2+0X4) = 37-(8+0) = 29 5. संशोधित भाज्य 29 में 5 का भाग देते हैं। भागफल = 5, को रेखा के नीचे लिखते हैं, यह भागफल का दूसरा अंक होगा तथा शेषफल = 4 को मध्य खण्ड़ के 9 से पहले व नीचे लिखते हैं। अतः नया भाज्य = 49 होगा 6. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 49-(2X5+4X4) = 49-(10+16) = 23 7. संशोधित भाज्य 23 में 5 का भाग देते हैं। भागफल = 4 को रेखा के नीचे लिखते हैं, यह भागफल का तीसरा अंक होगा तथा शेषफल = 3 को तृतीय खण्ड़ के 6 से पहले व नीचे लिखते हैं। 8. अन्तिम शेषफल निम्न प्रकार से ज्ञात करते हैं। = 363-[(4X2+5X4)10-(4X4) = 363-(28X10)-16 = 363-280-16 = 363-296 =67 9. अतः भागफल = 454 तथा शेषफल = 67 |
|
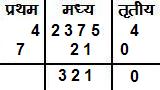
Example: 23754 ÷ 74
|
|
संकेत- 1. मध्य खण्ड़ के 23 में 7 का भाग देते हैं। 2. भागफल = 3 को रेखा के नीचे लिखते हैं, यह भागफल का प्रथम अंक होगा तथा शेषफल = 2 को मध्य खण्ड़ के 7 से पहले व नीचे लिखते हैं, नया भाज्य = 27 3. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 27-(3X4) =27-12 =15 |
|
4. 15 में 7 का भाग देते हैं। 5. भागफल =2 को रेखा के नीचे लिखते हैं, यह भागफल का दूसरा अंक होगा तथस शेषफल =1 को मध्य खण्ड़ के 5 से पहले व नीचे लिखते हैं, नया भाज्य = 15 6. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 15-(2X4) =15-8 =7 7. 7 में 7 का भाग देते हैं। 8. भागफल = 1 को रेखा के नीचे लिखते हैं, यह भागफल का तीसरा अंक होगा तथा शेषफल =0 को तृतीय खण्ड़ के 4 से पहले व नीचे लिखते हैं, नया भाज्य = 04 9. संशोधित भाज्य = अन्तिम शेषफल = नया भाज्य – (भागफल X ध्वजांक) = 04-(1X4) =4-4 =0 10. अतः भागफल =321 तथा शेषफल =0
|
|
Example: 20675 ÷ 827
|
|
संकेत- 1. मध्य खण्ड़ के 206 में 82 का भाग देते हैं। 2. भागफल = 2 को रेखा के नीचे लिखते हैं, यह भागफल का प्रथम अंक होगा तथा शेषफल = 42 को मध्य खण्ड़ के 7 से पहले व नीचे लिखते हैं, नया भाज्य = 427 3. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 427-(2X7) =427-14 =413 |
|
4. 413 में 82 का भाग देते हैं। 5. भागफल = 5 को रेखा के नीचे लिखते हैं, यह भागफल का दूसरा अंक होगा तथस शेषफल = 3 को मध्य खण्ड़ के 5 से पहले व नीचे लिखते हैं, नया भाज्य = 35 6. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 35-(5X7) =35-35 =0 7. अतः भागफल =25 तथा शेषफल =0 |
|
Example: 342945 ÷ 125
|
|
संकेत- 1. मध्य खण्ड़ के 3 में 1 का भाग देते हैं। 2. भागफल =3 को रेखा के नीचे लिखते हैं, यह भागफल का प्रथम अंक होगा तथा शेषफल = 0 को मध्य खण्ड़ के 4 से पहले व नीचे लिखते हैं, नया भाज्य = 04 3. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 04-(3X2) =4-6 = – 2 क्योंकि संशोधित भाज्य ॠणात्मक आता हैं, अतः भागफल का प्रथम अंक 3 के स्थान पर 2 लेते हैं। इस कारण क्रियापद (ii) तथा (iii) निरस्त करने योग्य हैं। |
|
4. भागफल =2 को रेखा के नीचे लिखते हैं, यह भागफल का प्रथम अंक होगा तथा शेषफल = 1 को मध्य खण्ड़ के 4 से पहले व नीचे लिखते हैं, नया भाज्य = 14 5. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 14 – (2X2) =14 – 4 =10 6. 10 में 1 का भाग देते हैं। 7. भागफल = 7 (≠8, ≠9, ≠10 क्योंकि भागफल 8, 9, 10 लेने पर संशोधित भाज्य ॠणात्मक आता हैं) को रेखा के नीचे लिखते हैं,यह भागफल का दूसरा अंक होगा तथा शेषफल = 3 को मध्य खण्ड़ के 2 से पहले व नीचे लिखते हैं, नया भाज्य = 32 8. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 32-(7X2+2X5) =32-(14+10) =32-24 =8 9. 8 में 1 का भाग देते हैं। 10. भागफल =4 (≠5, ≠6, ≠7, ≠8 क्योंकि भागफल 5, 6, 7, 8 लेने पर संशोधित भाज्य ॠणात्मक आता हैंA) को रेखा के नीचे लिखते हैं, यह भागफल का तीसरा अंक होगा तथा शेषफल =4 को तृतीय खण्ड़ के 9 से पहले व नीचे लिखते हैं, नया भाज्य = 49 11. संशोधित भाज्य = नया भाज्य – (भागफल अंक X ध्वजांक) = 49-(4X2+7X5) =49-(8+35) =49-43 = 6 12. 6 में 1 का भाग देते हैं। 13. भागफल = 3 (≠4, ≠5, ≠6) को रेखा के नीचे लिखते है, यह भागफल का चौथा अंक होगा तथा शेषफल = 3 को तृतीय खण्ड़ के 4 से पहले व नीचे लिखते हैं। 14. अन्तिम शेषफल=345-[(3X2+4X5)10-(3X5) =345-(26X10)-15 =345-260-15 =345-275 =70 15. अतः भागफल =2743 तथा शेषफल =70 |
|